Kinematics and Kinetics: An Applied Interpretation
by Andrew Richardson
We have Linear and Angular variables which make up biomechanics and they too have their own sub sections.
Distance and Displacement
Distance (length of the path a body follows) and displacement (length of a straight line joining the start and finish points) are quantities used to describe a body's motion. e.g. in a 400m race on a 400m track the distance is 400 metres but their displacement will be zero metres (start and finish at the same point).
Speed and Velocity
Speed and velocity describe the rate at which a body moves from one location to another. Average speed of a body is obtained by dividing the distance by the time taken and average velocity is obtained by dividing the displacement by the time taken e.g. a swimmer in a 50m race in a 25m length pool who completes the race in 71 seconds - distance is 50m and displacement is 0m (swimmer is back where they started) so speed is 50/71= 0.70m/s and velocity is 0/71=0 m/s
Speed and Velocity = distance travelled ÷ time taken
Acceleration
Acceleration is defined as the rate at which velocity changes with respect to time.
average acceleration = (final velocity - initial velocity) ÷ elapsed time
From Newton's 2nd law:
Force = Mass x Acceleration (F=MA)
Acceleration = Force ÷ Mass (A = F/M)
If the mass of a sprinter is 60kg and the force exerted on the starting blocks is 600N then the acceleration is 600 ÷ 60 = 10 m/sec²
Acceleration due to gravity
Whilst a body is in the air it is subject to a downward acceleration, due to gravity (g), of approximately 9.81m/s²
Vectors and Scalars
Distance and speed can be described in terms of magnitude (amount) and are known as scalars. Displacement, velocity and acceleration require magnitude and direction and are known as vectors.
Components of a vector
Velocity Components
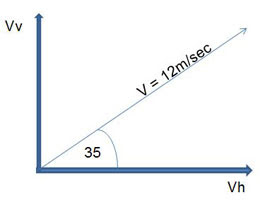
Figure 2
Let us consider the horizontal and vertical components of velocity of the medicine ball in Figure 1.
Figure 2 indicates the angle of release of the medicine ball is 35° and the velocity at release as 12 metres/second (m/sec).
Vertical component Vv = 12 x sin 35° = 6.88 m/sec
Horizontal component Vh = 12 x cos 35° = 9.82 m/sec
Let us now consider the distance the medicine ball will travel horizontally (its displacement).
Distance (D) = ((v² × sinØ × cosØ) + (v × cosØ × sqrt((v × sinØ)² + 2gh))) ÷ g
Where v = 12, Ø = 35, h = 2m (height of the shot above the ground at release) and g = 9.81
D = ((12² × sin35 × cos35) + (12 × cos35 × sqrt((12 × sin35)² + 2 x 9.81 x 2))) ÷ 9.81
D = 16.22m
Feel free to take a short break after reading that. Inb4 how do I even math bro........
Continuing on :)
The time of flight of the shot can be determined from the equation:
Time of flight = Distance (D) ÷ velocity (Vh)
Time of flight = 16.22 ÷ 9.82 = 1.65 seconds
Uniformly accelerated motion
When a body experiences the same acceleration throughout an interval of time, its acceleration is said to be constant or uniform and the following equations apply:
Final velocity = initial velocity + (acceleration x time)
Distance = (initial velocity x time) + (½ x acceleration x time²)
Moment of Force (torque)
The moment of force or torque (τ) is defined as the application of a force at a perpendicular distance to a joint or point of rotation.
Torque (τ = rFsin θ ) depends on three quantities:
the length of the lever arm connecting the axis to the point of force application (r)
the force applied (F)
the angle between the force vector and the lever arm (sin θ)
Angular Kinematics
Angular distance and displacement:
When a rotating body moves from one position to another, the angular distance through which it moves is equal to the length of the angular path. The angular displacement that a rotating body experiences is equal to the angle between the initial and final position of the body.
Angular movement is usually expressed in radians where 1 radian = 57.3°
Angular speed, velocity and acceleration
Angular speed = angular displacement ÷ time
Angular velocity = angular displacement ÷ time
Angular acceleration = (final angular velocity - initial angular velocity) ÷ time
Angular Momentum
Angular momentum is defined as: angular velocity x moment of inertia
The angular momentum of a system remains constant throughout a movement provided nothing outside of the system acts with a turning moment on it. This is known as the Law Conservation of Angular Momentum. (e.g. if a skater, when already spinning, moves their arms out to the side, then the rate of spin will change but the angular momentum will stay the same).
Linear Kinetics
Kinetics is concerned with what causes a body to move.
Momentum, inertia, mass, weight and force
Momentum: mass x velocity
Inertia: the reluctance of a body to change whatever it is doing.
Mass: the quantity of matter of which a body is composed of - not affected by gravity - measured in kilograms (kg).
Weight: force due to gravity -9.81m/s².
Force: a pushing or pulling action that causes a change of state (rest/motion) of a body is proportional to mass x acceleration. It is measured in Newtons (N) where 1N is the force that will produce an acceleration of 1 m/s² in a body of 1kg mass.
The classification of external or internal forces depends on the definition of the 'system'. In biomechanics, the body is seen as the 'system' so any force exerted by one part of the system on another part of the 'system' is known as an internal force all other forces are external.
Newton's Laws of Motion
First Law: Every body continues in its state of rest or motion in a straight line unless compelled to change that state by external forces exerted upon it.
Second Law: The rate of change of momentum of a body is proportional to the force causing it and the change takes place in the direction in which the force acts
Third Law: To every action there is an equal and opposite reaction OR for every force that is exerted by one body on another there is an equal and opposite force exerted by the second body on the first
Newton's law of gravitation
Any two particles of matter attract one another with a force directly proportional to the product of their masses and inversely proportional to the square of the distance between them
Kinetic Energy and Power
Kinetic energy is the mechanical energy possessed by a moving object.
Kinetic Energy = ½ x mass x velocity² (joules)
Power is defined as the rate at which energy is used or created from other forms
Power = energy used ÷ time taken
Power = (force x distance) ÷ time taken
Power = force x velocity
Angular Kinetics
Translation and couple
A force that acts through the centre of a body result in movement (translation). A force whose line of action which does not pass through the body's centre of gravity is called an eccentric force and results in movement and rotation.
Example - if you push through the centre of an object it will move forward in the direction of the force. if you push to one side of the object (eccentric force) it will move forward and rotate.
A couple is an arrangement of two equal and opposite forces that cause a body to rotate.
Levers
A lever is a rigid structure, hinged at one point and to which forces are applied at two other points. The hinge is known as the fulcrum. The two forces forces that act on the lever are the weight that opposes movement and a force that causes movements.
Length of resistance arm
Bernoulli Effect
If an object has a curved top and flat bottom (e.g. the wing of an aircraft), the air will have further to travel over the top of the wing than the bottom. For the two airflows to reach the rear of the wing at the same time the air flowing over the top of the wing will have to flow faster resulting in less pressure above the wing (air is thinner) than below it and the aircraft will lift. This is known as the Bernoulli effects.
What this article will achieve is the following:
I hope you enjoy it.
Now before we begin, there is a growing trend of lifters/coaches/athletes whom refuse to learn or educate themselves on the new training methods or the science/research of training methodologies. Their excuse is usually "nah I am old school", no you're just lazy. Don't be afraid to say "I don't know what something is", no one will think any less of you in fact they are more than likely to go and help you understand it. Embrace modern day theories and leaning. Don't shut yourself off from the science.
- A better understanding of what biomechanics is and not just a term "PT's" throw around to impress their clients
- The Difference between kinematics and kinetics - applying these principles to some sports (powerlifting, weightlifting etc.)
- Using biomechanics in a sports science/strength and conditioning application.
I hope you enjoy it.
Now before we begin, there is a growing trend of lifters/coaches/athletes whom refuse to learn or educate themselves on the new training methods or the science/research of training methodologies. Their excuse is usually "nah I am old school", no you're just lazy. Don't be afraid to say "I don't know what something is", no one will think any less of you in fact they are more than likely to go and help you understand it. Embrace modern day theories and leaning. Don't shut yourself off from the science.
Lets get started with some definitions shall we;
Biomechanics - The science concerned with the internal and external forces acting on the human body and the effects produced by these forces. So we have seen some biomechanical analysis of a counter-movement jump (vertical jump) or a squat.
Kinematics: - The branch of biomechanics concerned with the study of movement from a geometrical point of view. This can be described as a phase analysis of a movement e.g basketball.
Kinetics - The branch of biomechanics concerned with what causes a body to move the way it does. as well as what forces are acting upon the body and cause it to move in its own way
We have Linear and Angular variables which make up biomechanics and they too have their own sub sections.
Distance and Displacement
Distance (length of the path a body follows) and displacement (length of a straight line joining the start and finish points) are quantities used to describe a body's motion. e.g. in a 400m race on a 400m track the distance is 400 metres but their displacement will be zero metres (start and finish at the same point).
Speed and Velocity
Speed and velocity describe the rate at which a body moves from one location to another. Average speed of a body is obtained by dividing the distance by the time taken and average velocity is obtained by dividing the displacement by the time taken e.g. a swimmer in a 50m race in a 25m length pool who completes the race in 71 seconds - distance is 50m and displacement is 0m (swimmer is back where they started) so speed is 50/71= 0.70m/s and velocity is 0/71=0 m/s
Speed and Velocity = distance travelled ÷ time taken
Acceleration
Acceleration is defined as the rate at which velocity changes with respect to time.
average acceleration = (final velocity - initial velocity) ÷ elapsed time
From Newton's 2nd law:
Force = Mass x Acceleration (F=MA)
Acceleration = Force ÷ Mass (A = F/M)
If the mass of a sprinter is 60kg and the force exerted on the starting blocks is 600N then the acceleration is 600 ÷ 60 = 10 m/sec²
Acceleration due to gravity
Whilst a body is in the air it is subject to a downward acceleration, due to gravity (g), of approximately 9.81m/s²
Vectors and Scalars
Distance and speed can be described in terms of magnitude (amount) and are known as scalars. Displacement, velocity and acceleration require magnitude and direction and are known as vectors.
Components of a vector
Chest Pass
Figure 1Velocity Components
Figure 2
Let us consider the horizontal and vertical components of velocity of the medicine ball in Figure 1.
Figure 2 indicates the angle of release of the medicine ball is 35° and the velocity at release as 12 metres/second (m/sec).
Vertical component Vv = 12 x sin 35° = 6.88 m/sec
Horizontal component Vh = 12 x cos 35° = 9.82 m/sec
Let us now consider the distance the medicine ball will travel horizontally (its displacement).
Distance (D) = ((v² × sinØ × cosØ) + (v × cosØ × sqrt((v × sinØ)² + 2gh))) ÷ g
Where v = 12, Ø = 35, h = 2m (height of the shot above the ground at release) and g = 9.81
D = ((12² × sin35 × cos35) + (12 × cos35 × sqrt((12 × sin35)² + 2 x 9.81 x 2))) ÷ 9.81
D = 16.22m
Feel free to take a short break after reading that. Inb4 how do I even math bro........
Continuing on :)
The time of flight of the shot can be determined from the equation:
Time of flight = Distance (D) ÷ velocity (Vh)
Time of flight = 16.22 ÷ 9.82 = 1.65 seconds
Uniformly accelerated motion
When a body experiences the same acceleration throughout an interval of time, its acceleration is said to be constant or uniform and the following equations apply:
Final velocity = initial velocity + (acceleration x time)
Distance = (initial velocity x time) + (½ x acceleration x time²)
Moment of Force (torque)
The moment of force or torque (τ) is defined as the application of a force at a perpendicular distance to a joint or point of rotation.
Torque (τ = rFsin θ ) depends on three quantities:
the length of the lever arm connecting the axis to the point of force application (r)
the force applied (F)
the angle between the force vector and the lever arm (sin θ)
Torque and length of lever arms
• Torque – (moment of force) the turning effect of an eccentric force
• Eccentric force - force applied in a direction not in line with the centre of rotation of an object with a fixed axis
– In objects without a fixed axis it is an applied force that is not in line with object's centre of gravity
• For rotation to occur an eccentric force must be applied
Torque and length of lever arms
• In humans, contracting muscle applies an eccentric force (not to be confused with eccentric contraction) to bone upon which it attaches & causes the bone to rotate about an axis at the joint
• Amount of torque is determined by multiplying amount of force (force magnitude) by force arm
Torque and length of lever arms
• Force arm - perpendicular distance between location of force application & axis
– a.k.a. moment arm or torque arm
– shortest distance from axis of rotation to the line of action of the force
– the greater the distance of force arm, the more torque produced by the force
Torque and length of lever arms
• Often, we purposely increase force arm length in order to increase torque so that we can more easily move a relatively large resistance (increasing our leverage).
• Resistance arm - distance between the axis and the point of resistance application.
Torque and length of lever arms
• Inverse relationship between length of the two lever arms.
– Between force & force arm.
– Between resistance & resistance arm.
– The longer the force arm, the less force required to move the lever if the resistance
& resistance arm remain constant.
– Shortening the resistance arm allows a greater resistance to be moved if force & force arm remain constant.
Torque and length of lever arms
• Proportional relationship between force components & resistance components.
– If either of the resistance components increase, there must be an increase in one or both of force component.s
– Greater resistance or resistance arm requires greater force or longer force arm.
– Greater force or force arm allows a greater amount of resistance to be moved or a longer resistance arm to be used.
Torque and length of lever arms
• Even slight variations in the location of the force and resistance are important in determining the effective force of the muscle.
Torque and length of lever arms
• Human leverage system is built for speed & range of movement at expense of force
• Short force arms & long resistance arms require great muscular strength to produce movement
• Ex. biceps & triceps attachments
– biceps force arm is 1 to 2 inches.
– triceps force arm less than 1 inch.
Torque and length of lever arms
• Human leverage for sport skills requires several levers
– throwing a ball involves levers at shoulder, elbow & wrist joints.
• The longer the lever, the more effective it is in imparting velocity
– A tennis player can hit a tennis ball harder with a straight-arm drive than with a bent elbow because the lever (including the racket) is longer & moves at a faster speed.
Torque and length of lever arms
• Long levers produce more linear force and thus better performance in some sports such as baseball, hockey, golf, field hockey, etc.
Torque and length of lever arms
• For quickness, it is desirable to have a short lever arm
– baseball catcher brings his hand back to his ear to secure a quick throw.
– sprinter shortens his knee lever through flexion that he almost catches his spikes in his gluteal muscles.
Angular Kinematics
Angular distance and displacement:
When a rotating body moves from one position to another, the angular distance through which it moves is equal to the length of the angular path. The angular displacement that a rotating body experiences is equal to the angle between the initial and final position of the body.
Angular movement is usually expressed in radians where 1 radian = 57.3°
Angular speed, velocity and acceleration
Angular speed = angular displacement ÷ time
Angular velocity = angular displacement ÷ time
Angular acceleration = (final angular velocity - initial angular velocity) ÷ time
Angular Momentum
Angular momentum is defined as: angular velocity x moment of inertia
The angular momentum of a system remains constant throughout a movement provided nothing outside of the system acts with a turning moment on it. This is known as the Law Conservation of Angular Momentum. (e.g. if a skater, when already spinning, moves their arms out to the side, then the rate of spin will change but the angular momentum will stay the same).
Linear Kinetics
Kinetics is concerned with what causes a body to move.
Momentum, inertia, mass, weight and force
Momentum: mass x velocity
Inertia: the reluctance of a body to change whatever it is doing.
Mass: the quantity of matter of which a body is composed of - not affected by gravity - measured in kilograms (kg).
Weight: force due to gravity -9.81m/s².
Force: a pushing or pulling action that causes a change of state (rest/motion) of a body is proportional to mass x acceleration. It is measured in Newtons (N) where 1N is the force that will produce an acceleration of 1 m/s² in a body of 1kg mass.
The classification of external or internal forces depends on the definition of the 'system'. In biomechanics, the body is seen as the 'system' so any force exerted by one part of the system on another part of the 'system' is known as an internal force all other forces are external.
Newton's Laws of Motion
First Law: Every body continues in its state of rest or motion in a straight line unless compelled to change that state by external forces exerted upon it.
Second Law: The rate of change of momentum of a body is proportional to the force causing it and the change takes place in the direction in which the force acts
Third Law: To every action there is an equal and opposite reaction OR for every force that is exerted by one body on another there is an equal and opposite force exerted by the second body on the first
Newton's law of gravitation
Any two particles of matter attract one another with a force directly proportional to the product of their masses and inversely proportional to the square of the distance between them
Kinetic Energy and Power
Kinetic energy is the mechanical energy possessed by a moving object.
Kinetic Energy = ½ x mass x velocity² (joules)
Power is defined as the rate at which energy is used or created from other forms
Power = energy used ÷ time taken
Power = (force x distance) ÷ time taken
Power = force x velocity
Angular Kinetics
Translation and couple
A force that acts through the centre of a body result in movement (translation). A force whose line of action which does not pass through the body's centre of gravity is called an eccentric force and results in movement and rotation.
Example - if you push through the centre of an object it will move forward in the direction of the force. if you push to one side of the object (eccentric force) it will move forward and rotate.
A couple is an arrangement of two equal and opposite forces that cause a body to rotate.
Levers
A lever is a rigid structure, hinged at one point and to which forces are applied at two other points. The hinge is known as the fulcrum. The two forces forces that act on the lever are the weight that opposes movement and a force that causes movements.
Levers
The mechanical advantage of levers may be determined using the following equations:
Mechanical Advantage = Resistance Force OR Mechanical advantage = Length of force arm
Length of resistance arm
First-class Levers
• Produce balanced movements when axis is midway between force & resistance (i.e. a seesaw)
• Produce speed & range of motion when axis is close to force, (triceps in elbow extension)
• Produce force motion when axis is close to resistance (crowbar)
Second Class Levers
Produces force movements, since a large resistance can be moved by a relatively small force
– Wheelbarrow
– Nutcracker
– Loosening a lug nut
– Raising the body up on the toes
Third-class Levers
• Produce speed & range-of-motion movements
• Most common in human body
• Requires a great deal of force to move even a small resistance
– Paddling a boat
– Shovelling - application of lifting force to a shovel handle with lower hand while upper hand on shovel handle serves as axis of rotation.
Bernoulli Effect
If an object has a curved top and flat bottom (e.g. the wing of an aircraft), the air will have further to travel over the top of the wing than the bottom. For the two airflows to reach the rear of the wing at the same time the air flowing over the top of the wing will have to flow faster resulting in less pressure above the wing (air is thinner) than below it and the aircraft will lift. This is known as the Bernoulli effects.
Methods of Data Collection within Biomechanics include the following;
- Anthropometric parameters (weight, height, limb lengths, joint markers)
- Segmental kinematics (stereophotogrammetry, wearable sensors, etc)
- External forces and moments (dynamometry, baropodometry, etc)
- Muscular electrical activity (electromyography)
- Metabolic energy (indirect calorimetry)
- Simply using Dartfish, VICON an or an app which tracks
Looking at Biomechanics in Powerlifting specifically the squat with the help of the images;
We can see some examples of squatting. What we should be trying to do is load the hips/hamstrings more and less anterior sheer force on the knee (don't load the front of the knee, patella tendon/acl). The knee isn't as good as dealing with load when compared to the hip. The hip is much better as it is supported by a lot more muscles than the knee.
So when we say less anterior sheer force at the knee. What does that really mean? Well first it means limiting the amount of knee flexion (so knees tracking forwards). This will cause damage over the long term. Inexperienced coaches/personal trainers teach their clients inadequate technical demonstration of the lifts (squat) resulting in an increased risk of injury. In the squat that is not using the hips and excessively loading of the quadriceps muscles. This will limit their clients depth to parallel which from studies has the highest EMG activity in the quads but, one of the highest sheer force on the knee joint.
So to eliminate this, we should try to aim for a near vertical shin when squatting. That way we are taking the load off the knees and recruiting more muscles into the movement such as the hips, glutes and hamstrings. Is there anything wrong with having some knee tracking forward, no, not in the short term however in the long term I believe there will a negative strain put on the joint which may result in injury.
Now moving on to looking at the analysis of the bar path for 3 different squats. What a coach should remember is that the bar path should remain within a lifters own Base of Support (BOS). When using a weight (external load) this will alter the individuals centre of mass. This will try and force the subject outside their own base of support (BOS). When using weight (external load) it will have an effect on the subject’s perceived centre of mass (PCOM), which is the subject plus the external load. If the PCOM moves outside the BOS, then the squat will become more challenging and difficult.
If you look at all three pictures they all have different set ups based on the individual limb lengths, previous injuries, strengths/weaknesses etc. However the external load is always over the mid point of their feet. Never tracking too far forward or back. Staying in the middle of the BOS to generate as much force as physically possible. As you can tell as you go from left to right the shin angle becomes more and more vertical in nature as the bar position gets lowered this encourages a more posterior movement which again as I have said before it loads the hips.
All the power form any athlete comes form their hips and core (core in my eyes is defined as the pec down to the groin). A great way to train the core and hips is by doing box squats. Here is a great review of the exercise by my good friend Jay Farrant; https://www.facebook.com/JayFarrantCoach/posts/1068089763235735
As a sports scientist (to be) when I am looking at a squat;
The hip angle for two reasons, one being going below parallel to meet the demands of the sport and two, what is the relation of the hip to knee is it open/closed and or closer/further away from the knee.
Then I am looking at the knee and I am asking myself is it vertical, if not why not. What is influencing it. Finally the feet and back angle as this will affect the athletes centre of gravity/torque. But all this can be affected by individual levers.
We have just looked at some heavy terms and meanings within the world of Biomechanics, Here is a presentation myself and some of my fellow students did this year on a Biomechanical Analysis of the Jump Shot in Basketball. With this context it should make it easier to understand.
At University on my Applied Sport Science course we did a short presentation on looking at
"Can increasing the Knee flexion have a positive effect in the jump shot in Basketball"
by Andrew Richardson, Jonny Foulds and Clinton Oduor.
What we looked at included the following;
- Sport of Basketball
- Importance of a Basketball Jump Shot
- Basketball Jump Shot: Phase Analysis
- Basketball Jump Shot: Biomechanical Analysis
- Comparison of a Jump shot to a Countermovement Jump
- Does more Knee Flexion encourage a Positive/Negative Result
- Final Thoughts
- References
Sport of Basketball
The sport of basketball contains:
A combination of speed, quickness, power. A lot of energy goes through the knee joints in different movements within the sport e.g. layups, jump shot, rebounding, running, changes of direction. In this presentation the Jump Shot will be looked at.
The jump shot is; A shot with one or both hands in which a player leaps into the air and shoots the ball at the basket at the moment of reaching the highest point of the leap. (Dictionary.com)
Basketball players usually score points during the game using the jump shot (Struzik, Pietraszewski and Zawadzki, 2014) . For this reason, the jump shot is considered to be the most important element of technique in basketball and requires a high level of performance.
Due to it being such a highly used technique this may put added pressure through the knees (Struzik, Pietraszewiski and Zawadzki 2014)
Importance of a Jump shot
Requiring a high level of performance, the jump shot is considered the most important technique in basketball (Struzic, Bogdan & Zawadzki, 2014)
A two legged jump shot consists of more than 70% of an entire basketball game (Struzic, Bogdan & Zawadzki 2014)
Good technique of the Jump Shot means an increase in Jump Shot accuracy which increases the chances of scoring more points.
Basketball Jump Shot: Phase Analysis
There are 3 Phases of the Jump Shot (Babcock 2005)
1. Preparation/Stopping Phase
2. Shooting
- Fingertip Control
- Control the Ball
- Elbow alignment
- Jump
- Release
3. Follow Through
Preparation Phase:
When the player is Dribbling the ball towards the basket he will stop with a foot forward called the pivot foot. He cannot move this foot until he performs the shot or pass the ball to another player.
Shooting Phase:
Finger Tip Control; Basketball should be controlled by the finger tips the entire time whereas the palm of the hand does not touch the ball.
Controlling the Ball; The shooting hand controls the ball throughout the entire movement of the shot. The opposite hand should be placed on the side of the ball and sued for balance and control until the shot is released
Elbow Alignment; the elbow in the shooting arm should be close to the body and lined up with the target
Jump; The athlete jumps vertically in the air to perform the shot above the defender hand
Release; The release of the ball should be executed with a full arm extension and a flick of the wrist
Follow Through Phase:
A flick of the wrist and spread of the fingers should follow the final movement of the shot until the ball goes through the net
Following the ball through with the wrist and fingers it’s entire movement will give direction to the ball.
Full Phase Analysis of the Jump Shot
Basketball Jump Shot: Biomechanical Analysis
Below is an image of what the joints (ankle, Knee, Hip, Shoulder and Wrist) are doing during the 3 Phases of the Jump Shot at each specific Phase
Comparison of a Jump shot to a Countermovement Jump: A Valid Testing Measurement
Struzik, A., Bogdan, P. & Zawadzk (2014)
Biomechanical analysis of the jump shot in basketball
20 well trained junior division II basketball players
ground reaction forces measured using A Kistler force plate
Displacements of the upper level of the lower limbs measured with the BTS SMART using passive markers that reflect the emitted infrared radiation (IR).
markers were located at the greater femoral trochanters on both sides of the body.
6 cameras to capture at a frame rate of 120 Hz and 0.2 mm resolution
Subject performed a maximum CMJ without an arm swing (i.e., hands resting on hips) and a jump shot without the ball
Comparison of a Jump shot to a Countermovement Jump: A Valid Testing Measurement
Aim of this study “A kinematic profile of skills in professional basketball players” 2010, was to compare biomechanical characteristics of lower limbs in the takeoff and landing phases of a counter movement jump without an arm swing and a jumpshot
20 well-trained junior basketball players
Ground reaction forces measure with Kistler force plate
BioWare software used for each leg
Displacements of the upper level of the lower limbs were measured with the BTS SMART system
The system used 6 cameras to capture at a framerate of 120 Hz
Both movements produced similar curve profiles;
Landing force as twice the take-off force… potentially leading to injury.
Overuse injuries common in basketball
Lower extremity joint kinematics and structural parameters
were collected from 24 players from five professional basketball teams as
they performed manoeuvres typical of their sport.
Jump shot takeoff and jumpshot landing were looked at.
436.9 knee flexion velocity for the jump shot landing and the
layup landing, respectively. The most extreme knee extension was seen in the
jump takeoffs, with the jumpshot takeoff angle averaging -1 degrees, reflecting a completely extended knee.
Maximum knee extension on the jumpshot landing was 9.8 degrees also resulting in a practically straight leg
This could explain why the forces through this movement are so high.
Possibly a softer landing via a better knee flexion on landing
Possibly a softer landing via a better knee flexion on landing
Does more Knee Flexion in a Jump Shot Facilitate a better Performance
Yes and No
For an athlete to generate the most power and force from the jump. He/she must be within their Base of Support (BOS) ie between their feet. If they try and move their weight outside of the midpoint of their own BOS then they will not be able to produce as much force.
By this train of thought having more flexion (per individual) would not increase jump height or a basketball performance. This is due to the increase of load on the knee, increasing the anterior sheer forces which will limit knee and hip extension to carry out a full Jump Shot.
Knee flexion should not exceed similar angles to a CMJ as this will inhibit the power generated from the athlete making him/her rely more on their arms. Which in the sport of basketball you are taught form this position (see image).
Concluding Thoughts
The jump shot is a skill that involves total body movement
All the phases of the jump shot are important for accurate scoring results
A biomechanical analysis can help the athlete improve technique & form of the jump shot
From this it is possible to say the CMJ without an armswing maybe a good measure of the jumping abilities of the basketball players performing the jump shot.
High impact ratios and landing forces suggest the necessity of a greater emphasis on soft landing in basketball. Therefore it is possible that an increase in knee flexion may have a positive effect on the jump shot, not through performance but on injury prevention.
I hope you enjoyed reading this and it has given you a better understanding of what Biomechanics really is and what it entails.
References
Babcock, R. (2005). Shooting Fundamentals. Retrieved from: www.raptors.com/basketballdevelopment.1-10 [http://www.raptors.com/basketballdevelopment.1-10]
Jump Shot (n.d.) In Dictionary.com online. Retrieved from: http://dictionary.reference
McClay, I. S., Robinson, J. R., Andriacchi, T. P., Frederick, E. C., Gross, T., Martin, P. E., ... & Cavanagh, P. R. (2010). A kinematic profile of skills in professional basketball players. JAB, 10(3).
McGinnis, P.M., (2013). Biomechanics of Sport and Exercise. Champaingn,IL.
Struzik, A., Bogdan, P. & Zawadzk (2014). Biomechanical analysis of the jump shot. Journal of Human Kinetics, 42(1), 73-79.
HAY, J.G. (1993) The Biomechanics of Sports Technique. 4th Ed. London, Prentice-Hall International (UK) Ltd. p. 64-68
HAY, J.G. (1993) The Biomechanics of Sports Technique. 4th Ed. London, Prentice-Hall International (UK) Ltd. p. 64-68
Andrew Richardson, Founder of Strength is Never a Weakness Blog
I have a BSc (Hons) in Applied Sport Science and a Merit in my MSc in Sport and Exercise Science and I passed my PGCE at Teesside University.
Now I will be commencing my PhD into "Investigating Sedentary Lifestyles of the Tees Valley" this October 2019.
I am employed by Teesside University Sport and WellBeing Department as a PT/Fitness Instructor.
My long term goal is to become a Sport Science and/or Sport and Exercise Lecturer. I am also keen to contribute to academia via continued research in a quest for new knowledge.
My most recent publications:
My passion is for Sport Science which has led to additional interests incorporating Sports Psychology, Body Dysmorphia, AAS, Doping and Strength and Conditioning.
Within these respective fields, I have a passion for Strength Training, Fitness Testing, Periodisation and Tapering.
I write for numerous websites across the UK and Ireland including my own blog Strength is Never a Weakness.
I had my own business for providing training plans for teams and athletes.
I was one of the Irish National Coaches for Powerlifting, and have attained two 3rd places at the first World University Championships,
in Belarus in July 2016.Feel free to email me or call me as I am always looking for the next challenge.
Contact details below;
Facebook: Andrew Richardson (search for)
Facebook Page: @StrengthisNeveraWeakness
Twitter: @arichie17
Instagram: @arichiepowerlifting
Snapchat: @andypowerlifter
Email: a.s.richardson@tees.ac.uk
Linkedin: https://www.linkedin.com/in/andrew-richardson-b0039278
Research Gate: https://www.researchgate.net/profile/Andrew_Richardson7